SC junctions
A superconducting junction is a junction of a superconductor with another normal-conductive material or a superconductor with another normal-conductive material. The former is called a normal-conductor/superconductor junction and the latter a superconductor-superconductor junction or Josephson junction. Superconductors have an energy gap on the Fermi surface. The study of superconductor-superconductor junctions is important from the viewpoint of application, because it is necessary to know the properties of junctions when applying superconductors to electronics. The physics of superconducting junctions is also important from the viewpoint of symmetry, edge states, and topological quantum phenomena in superconductors.
-
Normal metal/superconductor junction and Andreev reflection
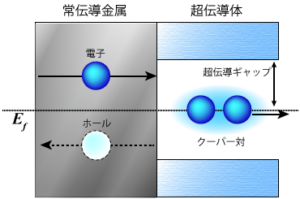 At a normal metal/superconductor junction, electrons incident from a normal metal cannot tunnel as quasiparticles if their energy is within the energy gap of the superconductor. At the interface with the superconductor there is not only the usual reflection, but also the Andreev reflection, where the incident electron is reflected as a hole at the interface with the superconductor. The Andreev reflection forms Cooper pairs in the superconductor. This process was predicted by Andreev in 1964 and is essential for understanding the transport properties of normal-superconductor junctions. The theory of Andreev reflection was extended to the transport properties of superconducting junctions by Blonder, Tinkham and Klapwijk in 1982. When a junction transmissivity is unity, perfect Andreev reflection occurs, and the probability of Andreev reflection is suppressed at lower transmissivities.
At a normal metal/superconductor junction, electrons incident from a normal metal cannot tunnel as quasiparticles if their energy is within the energy gap of the superconductor. At the interface with the superconductor there is not only the usual reflection, but also the Andreev reflection, where the incident electron is reflected as a hole at the interface with the superconductor. The Andreev reflection forms Cooper pairs in the superconductor. This process was predicted by Andreev in 1964 and is essential for understanding the transport properties of normal-superconductor junctions. The theory of Andreev reflection was extended to the transport properties of superconducting junctions by Blonder, Tinkham and Klapwijk in 1982. When a junction transmissivity is unity, perfect Andreev reflection occurs, and the probability of Andreev reflection is suppressed at lower transmissivities. -
Josephson junction
In a system consisting of a superconductor/superconductor junction, a superconducting current flows that depends on the macroscopic phase difference between the two superconductors. This current is a dissipationless current that flows without voltage. This breakthrough effect was predicted by Josephson in 1962, and many experiments have been conducted since then. When the permeability of the two superconductors is low, the dc Josephson current is proportional to sinφ, but when the permeability is high, the effect of the harmonic sin(nφ) becomes important, and the waveform of the current phase difference dependence is significantly different from the typical sin shape. Theoretical studies of the Josephson effect have been carried out in various ways, but the theory of the Josephson current has made great progress since the appearance of the systematic representation of the Josephson current using the Andreyev reflection coefficient by Furusaki and Tsukada in the early 1990s.
-
Andreev bound state
It has been known since the 1960s that in inhomogeneous superconducting systems such as superconducting junctions and flux cores, there exists a state in the gap called the Andreev bound state (ABS) due to the interference between electrons and holes. In the Josephson junction of a superconductor and a superconductor, the Andreev bound state can be used to describe the Josephson current, as was known in the work of Biehnecker et al. in the 1990s. In spin-singlet superconductors, Andreev bound states do not generally exist at the superconducting surface. However, in anisotropic superconductors such as cuprate superconductors (the Cooper pair symmetry of cuprate superconductors has been shown to be d-wave), a zero-energy (midgap) state forms at the surface. The zero-energy state appears as a zero-bias voltage conductance peak in tunneling spectroscopy of the normal metal-superconductor junction, and its existence is widely known today as a hallmark of anisotropic superconductors. The study of tunneling spectroscopy of anisotropic superconductors has since evolved into today’s research on Mayorana fermions.
Related Articles
- Y. Tanaka and S. Kashwiaya, Phys. Rev. Lett. 74 3451 (1995).
- S. Kashiwaya and Y. Tanaka. Rep. Prog. Phys. 63 1641 (2000).
- Y. Tanaka, T. Yokoyama and N. Nagaosa, Phys. Rev. Lett. 103, 107002 (2009).
-
Proximity effect
In systems where a metal and a superconductor are bonded together, Cooper pairs penetrate into the metal. This effect is called the proximity effect. The electron-hole interference effect and the proximity effect, which create the Andreev reflection, are two sides of the same coin. When the metal is in the diffuse conduction regime, the resistance of the metal-superconductor junction system is not simply the sum of the bulk metal value and the interface resistance. The resistance of the metal is generally smaller due to the intruding Cooper pair. The Usadel equation is a very useful method for calculating the resistance due to such proximity effects. Originally developed by Larkin et al. and advanced by Volkov, Nazarov et al. in the 1990s with advances in mesoscopic superconductivity.
-
Odd-frequency Cooper pair
It is widely known that the Cooper pair responsible for the superconducting state consists of two electrons. Many textbooks on Cooper pair symmetry state the following. The two-electron pair function (pair amplitude) according to the Fermi-Dirac statistics must be antisymmetric with respect to the contemporaneous interchange of the two electrons that compose it. This is because it must be consistent with the Fermi-Dirac statistics. Cooper pair symmetries are classified into spin-singlet even-parity (e.g., s- or d-wave) and spin-triplet odd-parity (e.g., p-wave). This classification focuses on Cooper pairs (two-electron correlations) formed at the same time. However, when the pair function is Fourier transformed with respect to the relative time of the two electrons and displayed in frequency, it is possible in principle for the pair function to have a frequency dependence. Such a case is classified as spin-triplet even-parity or spin-singlet odd-parity. In summary, if the pair function is an even function of frequency, the symmetry of the Cooper pair is classified as spin-singlet even parity and spin-triplet odd parity as before, and if the pair function is an odd function of frequency, it is classified as spin-triplet even parity and spin-singlet odd parity. The possible Cooper pair classifications are shown in the table below.
Frequency (time) Spin Orbit Total Superconducting state ESE +(odd) ー(singlet) +(even) ー(odd) Metallic superconductivity, copper oxide ETO +(even) +(triplet) ー(odd) ー(odd) Helium-3, Sr2RuO4 OTE ー(odd) +(triplet) +(even) ー(odd) Unidentified in bulk OSO ー(odd) ー(singlet) ー(odd) ー(odd) Unidentified in bulk ESE, ETO, OTE, and OSO stand for even-frequency spin-singlet even-parity, even-frequency spin-triplet odd-parity, odd-frequency spin-triplet even-parity, and odd-frequency spin-singlet odd-parity, respectively. The odd-frequency Cooper pair (OTE s-wave) was proposed by Berezinskii in 1974. It is difficult to conceive of such a pairing in the bulk superconducting state, and no odd-frequency bulk superconductor has yet been discovered.
However, symmetry breaking allows odd-frequency pairs to mix as subdominant pairs even though the major Cooper pairs are conventional even-frequency pairs. Translational symmetry breaking reveals that odd-frequency Cooper pairs are universally mixed with even-frequency Cooper pairs in inhomogeneous superconductors.
Bulk symmetry Andreev bound state Symmetry at interface ESE(s, dx2-y2-wave) 
No ESE+(OSO) ESE(dxy-wave) 
Yes OSO+(ESE) ETO(px-wave) 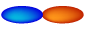
Yes OTE+(ETO) ETO(py-wave) 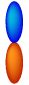
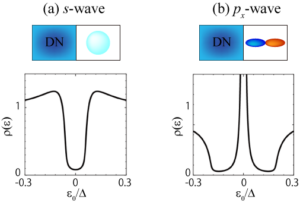
No ETO+(OTE) Bulk symmetry and symmetry at the interface (surface) are summarized in the table above. The entity of the midgap Andreev bound state is the odd-frequency Cooper pair itself. The midgap Andreyev bound state on the surface of a d-wave superconductor is odd-frequency p-wave, whereas that on the surface of a p-wave superconductor is odd-frequency s-wave. This causes an anomalous proximity effect in the spin-triplet p-wave superconductor-normal-conducting metal junction, where odd-frequency s-waves formed at the interface penetrate into the normal-conducting region (diffuse-conducting region with significant impurity scattering). This anomalous proximity effect is extremely unique in that the quasiparticle density of states ρ peaks at zero energy (see figure below), and is completely different from the conventionally known proximity effect in which the quasiparticle density of states has a gap at zero energy. Anomalous electromagnetic response phenomena are expected when odd-frequency pairs exist, and have been widely studied from this point of view.
Related Articles- Y. Tanaka, A. A. Golubov, S. Kashiwaya, and M. Ueda: Phys. Rev. Lett. 99 (2007) 037005.
- Y. Tanaka, Y. Tanuma, and A. A. Golubov: Phys. Rev. B 76 (2007) 054522.
- Y. Tanaka and A. A. Golubov: Phys. Rev. Lett. 98 (2007) 037003.
- Y. Tanaka and S. Kashiwaya: Phys. Rev. B 70 (2004) 012507.
- Y. Asano, A. A. Golubov, Y. V. Fominov, and Y. Tanaka: Phys. Rev. Lett. 107 (2011) 087001.
- T. Yokoyama, Y. Tanaka, and N. Nagaosa: Phys. Rev. Lett. 106 (2011) 246601.
- Y. Tanaka, Y. Asano, A. Golubov, and S. Kashiwaya: Phys. Rev. B 72 (2005) 140503(R).
- Y. Tanaka, M. Sato and N. Nagaosa, J. Phys. Soc. Jpn., 81, 011013 (2012).
-
Mechanism
Superconductivity is a phenomenon in which electrical resistance becomes zero below the transition temperature, and was discovered by Heike Kamerlingh Onnes in 1911. In 1933, it was discovered that, unlike the normal-conductive phase of metals in which the electrical resistance is virtually zero (perfect conductive phase), superconductivity exhibits perfect antimagnetism, called the Meissner effect. On the other hand, the reason for superconductivity and the electronic state in the superconducting state had long been unknown since the discovery of superconductivity. However, the theory published by Bardeen, Cooper, and Schrieffer in 1957 (BCS theory) clarified the basic principles of the superconductivity mechanism. The following is a brief explanation of the BCS theory.
First, in the superconducting state, two electrons are paired. This pair is called a Cooper pair. Although electrons are Fermi particles, Cooper pairs of two paired electrons are bosons, so Cooper pairs can condense collectively (Bose condensation). This condensed state is a superconducting state. So how can electrons form Cooper pairs? In order for electrons to form a pair, there must be some kind of attractive force between electrons. Since there is originally a Coulomb repulsion between electrons, they cannot form Cooper pairs. In the BCS theory, phonons are used as the mechanism for the formation of this attraction. When negatively charged electrons move through a crystal lattice of positively charged nuclei, a distortion of the crystal lattice occurs (phonons). Since there is a bias toward positive charge in the distorted area compared to the rest of the crystal, another electron feels an effective attraction to that biased area. In other words, there is an effective attraction between the electrons, mediated by the phonon. This effective attraction forms Cooper pairs, which condense to form a superconducting state.

Thus, the basic mechanism of superconductivity was clarified by the BCS theory. However, unconventional superconductors, which have clearly different properties from those of superconductors based on the BCS mechanism, were discovered one after another following the discovery of heavy-fermion superconductors in 1978. A typical example is the copper oxide high-Tc superconductor discovered in 1986. In high-Tc superconductors, the attraction that creates Cooper pairs is not the electron-lattice interaction, but rather spin fluctuations in which the spins of electrons try to become antiparallel to each other. Iron-based superconductors discovered in 2008 have the second highest transition temperature after cuprate superconductors, and a theory of superconductivity mediated by orbital fluctuations has been proposed in addition to spin fluctuations.
In Sr₂RuO₄, which has the same crystal structure as cuprate superconductors, it has been experimentally observed that the electrons forming Cooper pairs are parallel to each other in the spin triplet state, but various theories have been proposed regarding the mechanism of this phenomenon, and no conclusion has been reached. Recently, superconductivity has been discovered in CuxBi2Se3, a carrier-doped topological insulator. This material has attracted attention as a candidate for topological superconductivity, but the mechanism of its occurrence is still unclear. In our laboratory, we are studying the mechanism by which such superconductivity forms Cooper pairs, i.e., the mechanism of superconductivity.
Topological materials
A topological structure is a spatial “field” structure that cannot be untied by continuous transformation. It is generally classified by an integer called a topological invariant, and structures with different invariants cannot be continuously transformed. Explained in this way, it tends to sound mathematically and awkward, but it is actually a very clear concept when you draw a diagram and think about it.
As an example, consider the classical XY spin in two-dimensional space. The order parameter, or “field,” is a unit vector oriented in the xy-plane that represents the direction of magnetization, and the degrees of freedom in which the vector can move (called “order parameter space”) can be represented by a unit circle. Now consider the spatial structure of magnetization as shown in Figures (a)-(c). None of these are defects where the direction of magnetization is not determined at the center. To classify them topologically, we examine the change in magnetization orientation along the yellow arrows surrounding the defects. The side of each figure shows how the magnetization orientation changes in order-variable space: in (a) (b) it circles the unit circle counterclockwise, while in (c) it circles clockwise. Since (a) and (b) have the same direction of rotation, these structures can shift in a continuous transformation, and in fact, rotating the magnetization structure in (a) by 90 degrees around an axis perpendicular to the screen at each point results in (b). On the other hand, (c) cannot shift continuously from (a) and (b) because the direction of rotation is opposite to that of (a) and (b). In other words, (a) and (b) are topologically equivalent structures, and (c) is topologically different. In this example, the structures can be classified by the “winding number,” which is the number of lapses in the ordered variable space while one laps around a defect in real space, with (a) and (b) having a winding number of 1 and (c) having a winding number of -1. Besides XY spin, any system whose order parameter space can be described by a unit circle (s-wave superconductivity, superfluid helium, liquid crystals, etc.) can be classified by the same argument, and topological classification is a universal concept independent of the system.
Next, let us extend the above discussion to consider the topological structure of the 3-dimensional unit vector (Heisenberg spin) in 3-dimensional space. In this case, the ordered variable space is a unit sphere that indicates the direction of the 3-dimensional unit vector. If there is a point defect in 3-dimensional space, the structure is classified by the number of times it covers the unit sphere, which is the field space, during one rotation of the sphere covering the point defect. A specific example is shown in Figure (d) and is called a monopole.
Expanding the sphere surrounding the monopole to a two-dimensional plane yields an interesting structure called a scarmion. Specifically, consider the projection shown in Figure (e). In other words, connect the north pole of the unit sphere to a point on the sphere (red circle) by a straight line, and place the magnetization at the point of the red circle at the intersection of the plane tangent to the south pole and this straight line (blue point). (For those familiar with complex functions, recall the relationship between the complex plane and the Riemann sphere.) The resulting structure is shown in Figure (f). It is a two-dimensional topological structure without defects, and it exists stably by imposing the boundary condition that the magnetization points upward at the boundary. Just as (a) and (b) were topologically equivalent, so are (f) and (g), both of which are called scarmions or skyrmions and are currently being actively studied in the field of physical properties.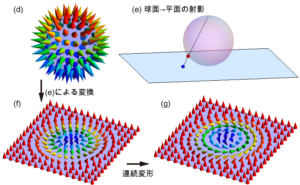
-
Topological insulators and topological crystal insulators
Topological insulator
Insulators with nontrivial values of topological invariants defined by the wave functions of electrons in solids are called topological insulators. On their surfaces, stable metallic states appear, the existence of which is guaranteed by topological invariants. Furthermore, topological invariants are physical quantities in the electromagnetic response and transport phenomena of the system. A typical example of a topological insulator is the quantum Hall effect that occurs in a two-dimensional electron system in a magnetic field. In this case, the quantum Hall conductivity is a topological invariant, and depending on its value, a metallic state exists at the edge of the system and a permanent current flows. The quantum Hall effect has long been a known example, but the recent discovery of its spin version, the quantum spin Hall effect, as well as topological insulators in three-dimensional systems, has since led to an explosion of research in this field. Interestingly, in three-dimensional topological insulators, magnetization (electric polarization) is induced by an electric field (magnetic field), resulting in an electromagnetic effect, and the polarization rate is predicted to be expressed as a topological invariant (i.e., quantized).
Topological crystal insulator
Quantum spin Hall insulators and three-dimensional topological insulators have Z2 topological invariants protected by time-reversal symmetry and the corresponding surface metallic states. On the other hand, it has been found that instead of time-reversal symmetry, topological invariants can also be defined by crystal symmetries such as rotations and mirror reflections. Systems in which these topological invariants have nontrivial values are called topological crystal insulators. In fact, in 2012, it was experimentally demonstrated that a topological crystal insulator state with mirror symmetry is realized in group IV-VI semiconductors. Not only this, further research is accelerating with the prediction of various materials and their classification theories being proposed.
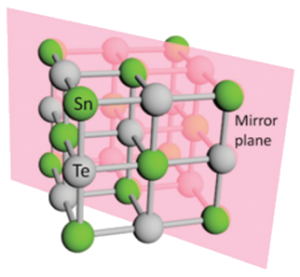
Related Articles- Y. Tanaka, et al., Nat. Phys. 8, 800 (2012); S.-Y. Xu, et al., Nat. Commun. 3, 1192 (2012); P. Dziawa, et al., Nat. Mater. 11, 1023 (2012).
-
Topological superconductor and topological crystal superconductor
Topological superconductor
When electrons form Cooper pairs, hybridization between electrons and holes occurs, opening an energy gap on the Fermi surface. This state is called a superconductor, and many metals are known to undergo a phase transition to a superconducting state at low temperatures. In the ground state of a superconductor, the states below the Fermi energy are completely packed, requiring a finite amount of energy to create fermionic excitations, thus achieving a state analogous to an insulator. Because of this similarity, states with a nonzero topological number of the ground-state wavefunction can be realized for superconducting states as well as for topological insulators, and are called topological superconductors. Topological superconductors are characterized by having Dirac excitations on their surfaces, called Majorana excitations, which are themselves antiparticles.
Topological crystal superconductor
Materials that realize superconductivity have a crystal symmetry that is unique to the material. This crystal symmetry allows the introduction of new topological numbers. In ordinary spin degenerate electron systems, the Mayrana excitations characteristic of topological superconductors always appear in pairs and have the same degrees of freedom as the Dirac excitations, so it has been thought that it would be difficult to demonstrate the unique properties of the Mayrana excitations. However, it has been shown that the unique properties of Mayrana excitations can be verified by using crystal symmetry.
-
Noncommutative Statistics and Majorana fermions
Non-Abelian statistics
In mathematics, when the operations of the elements according to an algebra are unordered, they are said to be commutative; when the exchange rule does not hold, they are said to be noncommutative. For example, an n×n matrix (n>1) is generally noncommutative. Noncommutative statistics refers to the statistical properties that some particles follow. In three-dimensional space, the statistical properties of particles are essentially divided into boson and fermion statistics, and the particles that follow those statistics are called bosons and fermions, respectively. Exchanging two particles does not change the wavefunction of a boson system, whereas the wavefunction of a fermion system is negatively signed.
$$\Psi_B(r_1, r_2)=\Psi_B(r_2, r_1),\ \ \ \Psi_F(r_1, r_2) = -\Psi_F(r_2, r_1)$$
On the other hand, in two-dimensional space, the wavefunction may depend on the orbit used for the exchange, and a general phase is attached to the wavefunction depending on the characteristics of the space.
$$\Psi_A(r_1, r_2)=e^{i\theta}\Psi_A(r_2, r_1)$$
Such particles are called anyons and follow fractional statistics. Mathematically, when dealing with the exchange of particles such as anyons, we define a group. The phase factor attached to the wave function is the representation of the group, which in this case is a complex number with absolute value 1. However, if there are three or more particles and degeneracy, the representation of the group is not a number, but a matrix that swaps and mixes degenerate states. Particles represented by such a group are called noncommutative anyons and are known to obey noncommutative statistics. Also, while most of these discussions have been done in lower dimensions, in three dimensions, a similar discussion can be done with textured rather than point particles.Majorana fermion
A Majorana fermion is a fermion whose particle and antiparticle are equal, which was theoretically proposed by E. Majorana in 1937. They exist as real solutions of the Dirac equation, and the particles and antiparticles represented by these solutions have no electric charge. Since they are mathematically real, they can be regarded as half of the usual fermions expressed in complex numbers. Although Majorana has theoretically demonstrated the existence of such a real number solution, no particle with such a property has yet been discovered. Currently, neutrinos and dark matter are candidates for such fermions, but no experimental confirmation has been obtained. Recently, however, the possibility of the existence of Majorana fermions has been pointed out in our field of condensed matter physics and has attracted considerable attention.
In superconductors, electrons and holes exist in a superposition state, and the number of quasiparticles is no longer constant. Therefore, charge is no longer a good quantum number, and quasiparticles of any charge can exist. In particular, zero charge quasiparticles can be realized if electrons and holes overlap perfectly. This condition is necessary to obtain an effective Majorana particle. However, the normal superconducting gap cannot achieve such a perfect superposition, and Majorana fermions are not expected to be realized. But the case of topological superconductivity is different. Topological superconductivity has a nontrivial gap, which closes at the edge of the superconductor, i.e., a zero-energy state is created at the edge. This state is a superposition of uncharged electrons and holes, corresponding to Majorana fermions. Whether or not topological superconductivity exists naturally is not a simple question, but recent experiments have artificially created such a state and observed what appears to be a Majorana quasiparticle as a peak in conductance. While this is not yet absolute proof, the results provide significant support for the existence of Majorana fermions in condensed matter systems.
Expectations for the Majorana particle realized in condensed matter are particularly high. The reason is that it is a quasiparticle that follows noncommutative statistics in low dimensions due to its nontrivial realization. Since it is a noncommutative anyon, it is considered to be robust to environmental noise, free of conventional decoherence, and capable of keeping quantum information in a very stable form. Therefore, it has been pointed out that it could be applied to future quantum computers as a topological qubit.
-
Monoatomic layer materials
Monoatomic layer materials are material systems consisting of a single layer of atoms. Since the realization of “graphene”, there has been an explosion of research, both theoretical and experimental, to realize materials that surpass graphene. Graphene, MoS2, and boron nitride (BN) are representative materials.
“Graphene”, the first monatomic layer material, was synthesized in 2004 and was awarded the Nobel Prize in Physics in 2010. Graphene is an extremely pure two-dimensional material consisting of carbon in a honeycomb lattice. It has a unique electronic structure as a zero-gap semiconductor, and the presence of Dirac fermions has been confirmed.Graphene is also a candidate for topological insulators, but its small spin-orbit interaction prevents it from being gapped, making it impossible to measure the quantum spin Hall effect at experimentally feasible temperatures. Therefore, “silicene,” “germanene,” and “stannene,” which are graphene-like materials composed of silicon, germanium, and tin, respectively, are attracting attention. These materials have a low buckle structure close to sp3 rather than a fully two-dimensional sp2 hybrid orbital, and thus exhibit new physical properties not found in graphene. Therefore, it is a candidate for two-dimensional topological insulators.
-
Weyl semimetal
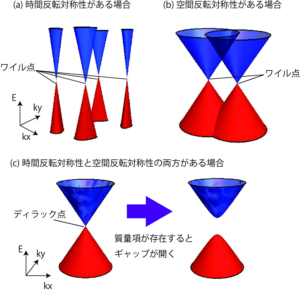
Electrons in Weyl semimetals behave like gapless Weyl fermions in relativity at low temperatures. In this case, the non-degenerate valence band and conduction band are in contact at a point, which is called the Weyl point. To obtain this Weyl point, at least time-reversal symmetry or space-reversal symmetry must be broken. This is because when time-reversal symmetry and space-reversal symmetry exist simultaneously, a double degeneracy (Kramers degeneracy) occurs at any k-point in the Brillouin zone, and the behavior near the contact point becomes a Dirac fermion instead of a Weil fermion. As explained in the next section, in the case of Dirac points, unless the k-point under consideration is at a special symmetry point, there exists a mass term that opens the gap, and the gap-opening state is stable due to band repulsion.
This argument can also be illustrated using topological numbers as follows. The behavior near the Weyl point can be effectively written as $$H(k)=v(k_x\sigma_x+k_y\sigma_y+k_z\sigma_z)$$. where v>0 is the Fermi velocity and σ is the Pauli matrix in spin space. As we can immediately see from the Hamiltonian, the wavenumber and spin direction are fixed. Thus, if we describe the expectation value of spin as a vector, it appears that a vector of spin is springing up around k=0. On the other hand, in the case of H(-k), the direction of the vector is reversed and the spin vector appears to be sucked into k=0. This upwelling and downwelling means that the topological numbers (Chern numbers) of the Weyl point are non-trivial, having C=+1 and C=-1, respectively. By analogy with electromagnetism, Weyl points with C=+1 and C=-1 are also called monopoles and antimonopoles in wavenumber space. From the periodic boundedness of the Brillouin zone, the sum of the Chern numbers must be zero (Nielsen-Nimiya theorem). Therefore, there are always pairs of monopoles and antimonopoles in the Brillouin zone. Let us now consider the stability of Weyl points by adding the previous discussion of time-reversal symmetry and space-reversal symmetry. First, in the case of time-reversal symmetry only, if we allow the transformation k→-k and σi→-σi for the time-reversal operation, there exist Weyl points with C=+1 at the k and -k points. There are also Weyl points with C=-1 at some k′ and -k′ points, since the antimonopole must also exist at the same time. Thus, in this case there are at least four Weyl points. Now consider the case where there is only space inversion symmetry. Under the space inversion operation, the wavenumber transforms from k to -k, but the spin is invariant. Therefore, there is a C=+1 Weyl point at the k point and a C=-1 Weyl point at the -k point. Thus, there are at least two Weyl points in this case. Finally, consider the case where both time-reversal and space-reversal symmetries exist. In this case, the above two cases can be combined and only the spin can be transformed as σi→-σi. Thus, there are simultaneously Weyl points with C=+1 and C=-1 at k points, which cancel each other. This means that topologically it becomes self-evident and it is possible to open the gap.
Fermi arcs appear on the surface due to the fact that Weyl points have non-trivial topological numbers. Fermi arcs are “arcs” of the Fermi surface that appear on the surface and connect Weyl points projected on the surface. Fermi arcs are an intrinsic property of Weil semimetals and provide strong evidence of Weil semimetals. Fermi arcs have also been observed in the recently discovered Weyl semimetals TaAs and NbAs with time-reversal symmetry by ARPES. Pyrochlore iridium oxides and HgCr22Se44 have also attracted attention as candidates for Weil semimetals. Various interesting phenomena such as anomalous Hall effect, chiral anomaly, and electro-magnetic effect have been theoretically predicted in Weyl semimetals, and they have been actively studied as next-generation topological materials in recent years.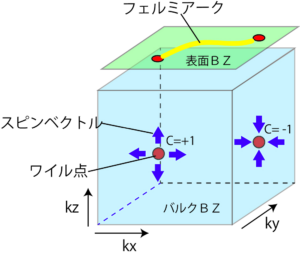 The simplest system to realize Weil semimetals is a superlattice structure of a topological insulator thin film and an ordinary insulator thin film doped with magnetic impurities. The time-reversal symmetry is broken by the magnetic impurity, and the direction of magnetization is oriented in the stacking direction. Thus, this system is a Weyl semimetal with space-reversal symmetry, and there are at least two Weyl points. Since each insulator is stacked as a thin film, the Dirac cones that appear on the surface of the topological insulator hybridize on the top and bottom surfaces. The parameters ΔT and ΔN, which express the degree of hybridization between the Dirac cones, correspond to the thickness of the topological insulator thin film and the normal insulator thin film, respectively. To be a Weil semimetal, the magnitude of magnetization of the magnetic impurity must be greater than |ΔT-ΔN|. Therefore, when |ΔT-ΔN| is small, it can become a Weil semimetal. In fact, one material with |ΔT-ΔN| close to zero is iPCM (superlattice phase-change memory). This material uses Sb2Te3 and GeTe as topological and normal insulators, respectively. One of the characteristics of this material is that it is known to undergo a phase transition from a phase with high electrical resistance to a phase with low electrical resistance as the temperature is increased. The electrical resistance difference between these two phases can be utilized as a memory, which has attracted industrial attention in recent years as a next-generation memory. First-principles calculations have pointed out that the value of |ΔT-ΔN| is almost zero in the high-resistance phase with time-reversal symmetry and space-reversal symmetry. Thus, if magnetic impurities can be doped so that the magnetization is oriented in the stacking direction, there is a possibility of Weil semimetals. However, so far there is no report that this has been realized.
The simplest system to realize Weil semimetals is a superlattice structure of a topological insulator thin film and an ordinary insulator thin film doped with magnetic impurities. The time-reversal symmetry is broken by the magnetic impurity, and the direction of magnetization is oriented in the stacking direction. Thus, this system is a Weyl semimetal with space-reversal symmetry, and there are at least two Weyl points. Since each insulator is stacked as a thin film, the Dirac cones that appear on the surface of the topological insulator hybridize on the top and bottom surfaces. The parameters ΔT and ΔN, which express the degree of hybridization between the Dirac cones, correspond to the thickness of the topological insulator thin film and the normal insulator thin film, respectively. To be a Weil semimetal, the magnitude of magnetization of the magnetic impurity must be greater than |ΔT-ΔN|. Therefore, when |ΔT-ΔN| is small, it can become a Weil semimetal. In fact, one material with |ΔT-ΔN| close to zero is iPCM (superlattice phase-change memory). This material uses Sb2Te3 and GeTe as topological and normal insulators, respectively. One of the characteristics of this material is that it is known to undergo a phase transition from a phase with high electrical resistance to a phase with low electrical resistance as the temperature is increased. The electrical resistance difference between these two phases can be utilized as a memory, which has attracted industrial attention in recent years as a next-generation memory. First-principles calculations have pointed out that the value of |ΔT-ΔN| is almost zero in the high-resistance phase with time-reversal symmetry and space-reversal symmetry. Thus, if magnetic impurities can be doped so that the magnetization is oriented in the stacking direction, there is a possibility of Weil semimetals. However, so far there is no report that this has been realized.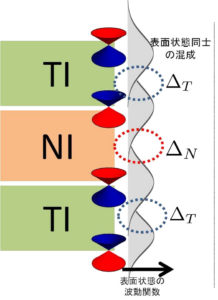 On the other hand, topological insulator thin films and insulator thin film superlattice structures are known to exhibit a Weyl semimetallic phase even when a potential difference is applied above and below the insulator thin film. The potential difference plays the role of breaking the spatial inversion symmetry. Therefore, the number of Weyl points depends on the discrete rotational symmetry with respect to the stacking direction, but since the Weyl semimetal has time-reversal symmetry, there are at least four Weyl points.
On the other hand, topological insulator thin films and insulator thin film superlattice structures are known to exhibit a Weyl semimetallic phase even when a potential difference is applied above and below the insulator thin film. The potential difference plays the role of breaking the spatial inversion symmetry. Therefore, the number of Weyl points depends on the discrete rotational symmetry with respect to the stacking direction, but since the Weyl semimetal has time-reversal symmetry, there are at least four Weyl points. -
Dirac semimetal
The Dirac semimetal appears when the time-reversal and space-reversal symmetries are preserved. It is doubly degenerate (Kramers degenerate) at any wavenumber k, and quadruply degenerate at the point of contact between the conduction band and the valence band (the Dirac point). Near the contact point, it is known to behave like a gapless Dirac fermion at low temperatures. As explained in the Weyl semimetal page, the Dirac point is topologically unprotected and can be easily gapped. Recently, however, it has been shown that stable Dirac points exist in the presence of crystal symmetry in addition to space and time reversal symmetries. Here we consider the case where the Dirac point is stabilized by the discrete rotation symmetry: Cn(n=2,3,4,6), with the recently discovered Dirac semimetal in mind. There are two major types of Dirac points protected by discrete rotation symmetry: one is the case where there is a single Dirac point at the time-reversal symmetry point (TRIM) at the Brillouin zone boundary, and the other is the case where there is a single Dirac point at the time-reversal symmetry point (TRIM) at the Brillouin zone boundary. In this case, the crystal must have non-conformal symmetry. Candidates of this type are β-cristobalite BiO2 (C4 symmetry) and distorted spinel structures (C2 symmetry). On the other hand, there is another case where two Dirac points appear on the symmetry axis. In this case, the Dirac points are located far from TRIM. This type of Dirac point has been experimentally observed by ARPES and STM in Bi3Na (C3 symmetry) [6-8] and Cd3As2 (C4 symmetry) materials. First-principles calculations have also shown the existence of Dirac points in A3Bi (A=Na, K, and Rb) and BaYBi (Y=Cu, Ag, and Au). In the latter type, when the surface is parallel to the axis of rotation, a surface state appears between the two Dirac points, as in the Weyl semimetals. In the case of Bi3Na, which is protected by C3, the Z2 topological number exists in the plane perpendicular to the axis of rotation and a pair of Fermi arcs appear. On the other hand, if it is protected by C4 like Cd3As2, there exists a nontrivial Miller-Chern number in the mirror plane perpendicular to the rotation axis and a Fermi loop appears. Unlike Fermi arcs, Fermi loops are not connected to Dirac points projected on the surface. The latter Dirac semimetals are often called “topological Dirac semimetals” because they have nontrivial surface states.
Dirac semimetals are expected to be capable of topological phase transitions to various topological phases such as topological insulators, topological superconductors, Weyl semimetals, and axion insulators. It is also attracting attention as a three-dimensional version of graphene, and has been observed to have high mobility and huge magnetoresistance.
- Axion insulator
Cold atoms
 When electrically neutral atoms are captured in a vacuum by light or a magnetic field and kept in a dilute gas state and cooled, they reach ultra-low temperatures as a gas without solidifying or liquefying. Recently, laser cooling and evaporative cooling technologies have realized such ultra-low temperature gases, which have attracted attention from both fundamental research and applications as quantum many-body systems that can be artificially controlled at will.
When electrically neutral atoms are captured in a vacuum by light or a magnetic field and kept in a dilute gas state and cooled, they reach ultra-low temperatures as a gas without solidifying or liquefying. Recently, laser cooling and evaporative cooling technologies have realized such ultra-low temperature gases, which have attracted attention from both fundamental research and applications as quantum many-body systems that can be artificially controlled at will.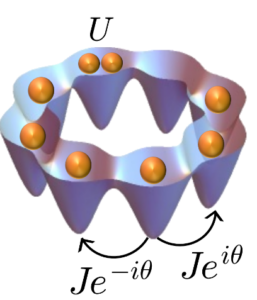 In addition, the response of macroscopic numbers of atoms in the measurement of magnetic fields and frequencies makes the sensitivity much higher, so that applications such as the development of high-sensitivity magnetometers and ultra-high-precision clocks that surpass atomic clocks are also expected. Thus, cooled atomic gases, which are highly manipulatable many-body quantum systems, are also called “artificial quantum gases” and provide a stage for studying a wide variety of physical phenomena depending on the setting. In our laboratory, we are engaged in a wide range of research on such systems, from quantitative calculations by numerical simulations to studies of mathematical physics such as topology, homotopy, and group theory. The following is a keyword explanation of the research topics handled in our laboratory.
In addition, the response of macroscopic numbers of atoms in the measurement of magnetic fields and frequencies makes the sensitivity much higher, so that applications such as the development of high-sensitivity magnetometers and ultra-high-precision clocks that surpass atomic clocks are also expected. Thus, cooled atomic gases, which are highly manipulatable many-body quantum systems, are also called “artificial quantum gases” and provide a stage for studying a wide variety of physical phenomena depending on the setting. In our laboratory, we are engaged in a wide range of research on such systems, from quantitative calculations by numerical simulations to studies of mathematical physics such as topology, homotopy, and group theory. The following is a keyword explanation of the research topics handled in our laboratory.-
Bose-Einstein Condensate (BEC)
When a population of Bose particles is cooled, Bose-Einstein condensation occurs, in which a macroscopic number of particles condense into a single quantum state. The material in which Bose condensation occurs is called Bose-Einstein condensate (BEC). Once Bose condensation occurs, a macroscopic number of particles condense into a single particle state, so that the entire population of particles behaves like a single wave, and quantum nature is noticeable. In superfluid helium, known since ancient times as BEC, the superfluid phenomenon of fluid flow with zero viscosity occurs, which is another consequence of the macroscopic wave function. In atomic gas BECs, the wavefunction can be directly observed using lasers, etc., and properties as matter waves, such as interference between two BECs and quantization of vortices, have been observed in experiments.
-
Spinor BEC
In atomic gases, BECs can be made from mixtures of two different Bose atoms or even a single atom with different spin states. BECs with such internal degrees of freedom require multiple components as order variables (wave functions that condense particles) and are called spinor BECs. In particular, when the internal degrees of freedom are real spins, an interesting situation called spin superfluidity is realized, where the spins are transported without dissipation as in a particle, or a particle flow is generated by a spatial change of spins. Recently, it has been discussed that by artificially creating spin-orbit interactions and complex spin-dependent gauge fields, a spin spatial structure similar to that of magnetic scirmions and nontrivial band structures similar to those of topological insulators can emerge.
Related Articles
-
Dipole BEC
Since the Coulomb interaction does not work for electrically neutral atoms, the interaction generally works only when two atoms come close together, about the size of an atom. However, when an atom has a large magnetic moment, the magnetic dipole-dipole interaction, which works far away, becomes dominant, and a completely different behavior is expected from that of conventional atomic gases. Recently, BECs of atoms with large magnetic moments such as Cr, Er, Dy, and Eu have been realized one after another, attracting attention as condensed matter with new physical properties. In particular, in BECs with spin degrees of freedom, spatial changes in spin orientation give rise to superfluid currents and complex interplay of spin, orbital, and gauge degrees of freedom. For example, after preparing a spin-polarized atomic gas in a magnetic field, turning off the magnetic field causes the Einstein-de Haas effect, in which the spin angular momentum is converted to orbital angular momentum and the condensate begins to rotate. This phenomenon is also evidence that the magnetic moment is a physical quantity called angular momentum, the same as rotational motion.
Related Articles
-
Non-Hermitian, Dynamic Instability
Usually, the Hamiltonian in quantum mechanics is Hermitian and the energy eigenvalues are real numbers. However, the excitation spectrum of BECs often has complex energies. This is because the energy spectrum of quasiparticles is described by a non-Hermitian matrix due to the exchange relation between the creation and annihilation operators of Bose particles. As the energy becomes complex, certain excitations grow exponentially with time, and the system becomes unstable. Such instability is called dynamical instability and has been observed experimentally under various circumstances. In recent research in condensed matter physics, many studies have been conducted to search for novel quantum states by phenomenologically describing interactions with the external world as non-Hermitian. It is an important system for elucidating the physical properties of non-Hermitian systems.
Related Articles
-
Floquet System / Driveline System
By applying external fields that oscillate periodically in time, such as electromagnetic waves and oscillating magnetic fields, to a system, it is possible to control the quantum state and its dynamics. It is well known that for spatially periodic systems, periodicity also appears in momentum space according to Bloch’s theorem, but according to Floquet’s theorem, which is the time version of Bloch’s theorem, periodicity appears in energy space for time-periodic systems. This is because under an oscillating external field, the system absorbs and emits (induces) energy ΔE corresponding to the frequency of the external field, causing the energy to be indefinite by an integer multiple of ΔE. In other words, applying an extravibrational field causes the spectrum to fold, creating a new band crossing. This can be used to control band topology, resonance phenomena, and dynamic instability on/off.
Related Articles
-
Topological phases
An insulator with an energy gap in the bulk can be divided into topologically non-trivial phases that can be continuously deformed into a trivial insulator (vacuum) and topologically non-trivial phases that cannot be continuously deformed into it, if we equate the systems that shift each other by continuous deformation that does not close the gap in the bulk. What is essential in this topological classification of phases is the existence of a “gap” in the distribution of eigenvalues of some matrix, and the details of the system are not important. In other words, topological phases are not limited to insulators, but can be realized in any system, including superconductors and cooled atomic systems. In recent years, the physics of topological phases has been actively studied not only in the equilibrium topological phases discussed above, but also in nonequilibrium systems such as Floquet and non-Hermite systems. In particular, cooled-atom systems, in which the parameters of the system and particle dissipation can be controlled with high precision, have attracted much attention as an ideal platform for realizing novel topological phases.
Related Articles
-
Open Quantum System
Ordinary quantum mechanics, described by the Schrödinger equation that you learned in your undergraduate classes, deals with isolated quantum systems, which are highly idealized situations where the system is disconnected from its environment, which is other physical systems.In contrast, in a real quantum system, the system is constantly interacting with its environment. Such a system is an open quantum system.For example, it is known that spontaneous emission, in which an atom (system) in an excited state spontaneously drops to a lower energy level while emitting light as it interacts with the vacuum (environment), must be treated as an open quantum system beyond the framework of Schrödinger equation.
-
Optical Lattice Systems and Dynamical Gauge Fields
In cooled atomic gases, the wave-like nature of light can be used to create ideal lattice systems. This system provides a platform for new experimental systems, since there are no photon oscillations (phonons) and the lattice spacing can be freely changed.Since we are dealing with electrically neutral atoms in experiments with cooled atomic systems, we cannot directly incorporate interactions such as electric fields (gauge fields). Therefore, it was proposed to introduce a virtual gauge field like the Aharonov-Bohm effect by applying a phase difference when jumping to an adjacent lattice site. Recently, U(1) gauge fields in electromagnetic fields have been reproduced in experiments, and the introduction of symmetric gauge fields such as SU(N) and Z₂ has also been proposed theoretically.
Magnetic skyrmions
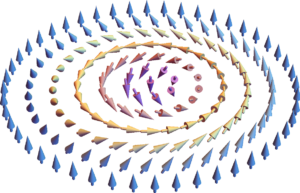 A magnetic skyrmion is a spatial structure in which the magnetization vector is as shown in the figure on the right in two-dimensional real space, and it exhibits the unique property that a large number of spins behave as if they were a single particle as a whole. This property is derived from the fact that the skyrmion structure is topologically stable, and the skyrmion cannot be unwound in a continuous deformation in which the amplitude of the magnetization at each point in space is kept finite and the boundary condition is satisfied (in the right figure, the magnetization is upward at the outer edge). In other words, once a skirmion is formed, it cannot disappear on its own and continues to exist stably.
A magnetic skyrmion is a spatial structure in which the magnetization vector is as shown in the figure on the right in two-dimensional real space, and it exhibits the unique property that a large number of spins behave as if they were a single particle as a whole. This property is derived from the fact that the skyrmion structure is topologically stable, and the skyrmion cannot be unwound in a continuous deformation in which the amplitude of the magnetization at each point in space is kept finite and the boundary condition is satisfied (in the right figure, the magnetization is upward at the outer edge). In other words, once a skirmion is formed, it cannot disappear on its own and continues to exist stably.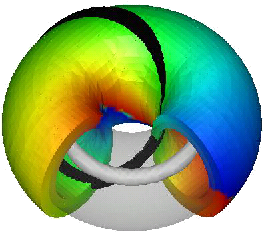 We have studied magnetization structures in chiral magnetic/ferromagnetic junction systems, control of inter-skirmion interactions, and dynamics of distorted skirmions due to crystal magnetic anisotropy. Recently, a new topological structure of the S² field in three-dimensional space, called Hopfion, has been observed and is of interest as a new topological structure. Hopfions are also one of the promising systems to be developed in the future. Hopfions have also been observed in cooled atomic gases by the method proposed by Kawaguchi before Hopfions in magnetic materials were discussed, making this a cross-disciplinary study.
We have studied magnetization structures in chiral magnetic/ferromagnetic junction systems, control of inter-skirmion interactions, and dynamics of distorted skirmions due to crystal magnetic anisotropy. Recently, a new topological structure of the S² field in three-dimensional space, called Hopfion, has been observed and is of interest as a new topological structure. Hopfions are also one of the promising systems to be developed in the future. Hopfions have also been observed in cooled atomic gases by the method proposed by Kawaguchi before Hopfions in magnetic materials were discussed, making this a cross-disciplinary study.Related Articles
- https://journals.aps.org/prb/abstract/10.1103/PhysRevB.93.064416
- https://journals.aps.org/prb/abstract/10.1103/PhysRevB.104.174446
- https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.100.180403
